Research interests of the group
The group investigates problems in statistical mechanics, hard and soft condensed-matter physics and lattice field theory with a focus on the application and advancement of cutting-edge numerical simulation and optimization techniques. Specifically, we are interested in complex systems where frustration effects and random disorder crucially shape the static and dynamic behavior. The major strands of current research are outlined below.

Hierarchical checkerboard decomposition of Ising lattice
High performance computing on GPUs
Over the last couple of years it has been realized that the vast computational power of graphics processing units (GPUs) could be harvested for purposes other than the video game industry. This power, which at least nominally exceeds that of current CPUs by large factors, results from the relative simplicity of the GPU architectures as compared to CPUs, combined with a large number of parallel processing units on single chip. To benefit from this setup for general computing purposes, the problems at hand need to be prepared in a way to profit from the inherent parallelism and hierarchical structure of memory accesses. Investigating possible advantages of GPU over CPU based systems for the case of studying classical spin models of statistical mechanics by Monte Carlo simulations, we find that only an explicit tailoring of the involved algorithms to the specific architecture under consideration allows to harvest the computational power of GPU systems. A number of examples, ranging from Metropolis simulations of ferromagnetic Ising models, over continuous Heisenberg and disordered spin-glass systems to parallel-tempering simulations have been investigated. Significant speed-ups by factors of up to 500 compared to serial CPU code as well as previous GPU implementations are observed.
Domain-walls defects in a continuous spin glass
Spin glasses and random-field systems with continuous spins
Spin glasses and random-field systems are models of disordered media with often highly counter-intuitive properties and an enormous number of experimental realisations in condensed matter physics, including highly frustrated magnets, superfluid helium, amorphous solids and ferroelectric materials. Novel phases of matter such as spin glasses, spin liquids and spin ices likely lie at the heart of several technologically important phenomena, such as high temperature superconductivity, colossal magnetoresistance, and the anomalous Hall effect. Besides, models of such systems have applications in seemingly rather distant fields such as the theory of associative memory, models of the immune system or error correcting codes. These applications and the theoreticians' interest in a novel and unconventional state of matter have prompted a large and ongoing research effort towards an understanding of the phenomena involved. Despite an early spectacular success in formulating and solving a mean-field theory revealing an astonishingly complex structure of the spin-glass phase, it was found a tricky and so-far elusive goal to ultimately decide about the relevance of these mean-field results for the real two- and three-dimensional systems realised experimentally. Due to its relative simplicity, most research has focused on the discrete Ising model of extreme spin-anisotropy, leading to some understanding of its low-temperature properties. The research pursued in the group aims at relaxing this simplification, investigating in detail spin glasses and random-field systems with continuous spins, which are often much more realistic for the experimentally realised systems.

Visualization of a dynamically triangulated manifold
Random surfaces and networks
Random graphs with internal geometric structure serve as models of membranes and random surfaces in statistical mechanics and condensed matter physics. This geometric structure is in contrast to the ensembles of generic random graphs without a well-defined topology considered in models, e.g., of the world-wide web. Coupling matter variables to such random structures has a disordering effect, for instance, on the magnetic ordering expected in pure systems. The Harris criterion judges the relevance of uncorrelated, quenched disorder for altering the universal properties of systems of statistical mechanics close to a continuous phase transition. In this case, a change of universality class is expected for models with a positive specific heat exponent α. A similar relevance criterion could be formulated for the case of spin models coupled to random graphs or lattices, and was extensively tested for the case of Poissonian Voronoi-Delaunay random graphs as well as the more drastically random dynamical triangulations model.
While these studies pertain to the case of quenched disorder, considering an ensemble of fixed random graphs, the case of annealed disorder, considering random graphs fluctuating on the time scale of the thermal fluctuations of spins, is of specific interest as well, in particular for graphs of the dynamical triangulations type, which in this form appear in a discrete, non-perturbative approach to a quantization of the gravitational interaction. Extensive recent studies of related problems are related to questions of cluster fractal dimensions on such graphs and on the effects of dynamical frustration induced by such graphs when coupled to antiferromagnetic spin models. Very similar effects occur in systems on small-world networks, where dynamical frustration leads to a dynamic adaptation of the network structure.

Optimization through extra dimensions
Optimization and simulation techniques for complex systems
Complex systems, including magnetic materials with frustration, such as spin glasses, but as well some random-graph models or even biopolymers, are most often characterized by a non-trivial energy landscape, featuring a large number of local minima separated by energy barriers. This structure can lead to extremely slow relaxation and a host of interesting dynamical phenomena such as ageing and memory. From the point-of-view of equilibrium statistical mechanics, however, this structure causes major methodological difficulties, in particular, for treating such systems numerically. The observed divergent autocorrelation times in Monte Carlo simulations and the vanishing probabilities for finding ground states in standard heuristic optimization approaches call for novel techniques for tackling these problems.
While a number of techniques for extended-ensemble Monte Carlo simulations and heuristic ground-state optimizations exist, many of the general-purpose techniques fail to perform satisfactorily for the hardest problems, including the case of the Edwards-Anderson spin glass. Here, special-purpose techniques are called for and, in particular, for the case of systems with continuous degrees of freedom efficient optimization techniques have only been invented very recently. These techniques have potential applications in many fields of science and engineering where global optimization problems are manifold, including the protein folding problem, traffic optimization, close packing, risk analysis, or circuit design.
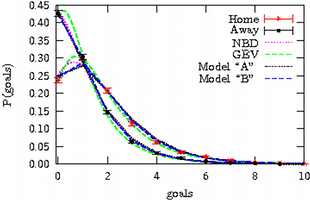
Modelling of football goal distributions
Statistical mechanics of social systems
Complex systems in social contexts have emerged in recent years as fields where the model-based point-of-view and methodological machinery of statistical mechanics might add a new perspective to the much more detailed investigations of more specific disciplines [47].
In a recent study, we have investigated the question of how the non-Gaussian form of goal statistics in ball games such as football can be understood from the microscopical perspective of the stochastic behaviour of co-operative “agents” (i.e., players) in abstract models. As it turned out, the distributions of goals scored by the home and away teams in football league and cup matches can be understood from a modified Bernoulli random process including a component of self-affirmation, i.e., a feedback of goal scoring on the subsequent scoring probabilities of the two teams. Depending on the update rules for the success probabilities, we arrive at a number of different “microscopic” models for the feedback process. In the continuum limit, one of these models can be shown to be equivalent to the negative binomial distribution, which had been previously applied with some success as a phenomenological description for the problem of modelling score data in sports. For all of the models, Pascal type recurrence relations allow to compute the exact probability distributions. A saddle-point calculation additionally yields astonishingly precise approximations for the large-N limit. Starting from these models, conclusions can be drawn for differences in the goal distributions observed between different leagues and cups. In particular, we considered the two separate German men’s premier leagues in the East and West during the cold war times and the unified league after 1990 to see how scoring in football and the component of self-affirmation depend on cultural and political circumstances.
A variety of situations in “social statistics” exist where either extremal value distributions have been observed or, on the other hand, “contagion” appears to modify elementary probabilities of occurring events according to the history of the individual or group considered by some feedback mechanism. For instance, the probability of a person to be affected by a (car, workplace, ...) accident rather naturally depends on the number or distance in time of previous accidents suffered. In other cases, probabilities will depend on the state of “neighbouring” agents, thus adding topological relations as observed in social network models to the feedback effects. Such systems deserve much more attention, promising an improved understanding from the perspective of mathematical statistics and statistical mechanics.